Framework

A Framework for Instructional Design

Robert Gagné's Nine Steps of Instruction

According to Robert Gagné (1985) there are nine events that provide a framework for an effective learning process:

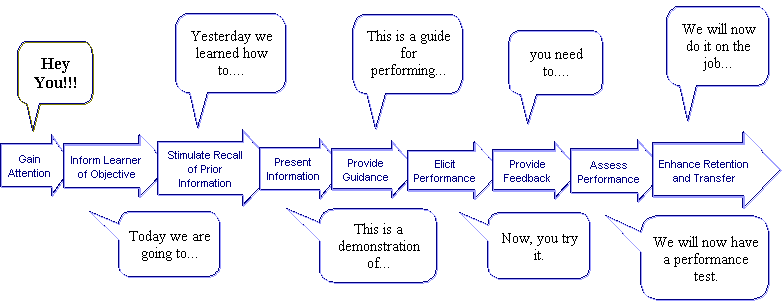
Robert Gagne's Nine Steps of Instruction

While Gagnés Nine Steps are often treated as iron clad rules, it has been noted for quite some time that the nine steps are more like a framework or guidelines:

“[Gagnés nine steps are] general considerations to be taken into account when designing instruction. Although some steps might need to be rearranged (or might be unnecessary) for certain types of lessons, the general set of considerations provide a good checklist of key design steps” (Good, Brophy, 1977).

The Nine Steps

1. Gain attention: Present a story, problem, or a new situation that will grab the learners' attention. This can be thought of as a interest device or teaser, such as the short segment often shown in a TV program right before the opening credits that keeps you watching the program. The ideal is to grab the learners' attention so that they will become involved in the learning process. You can use such interest devices as:

Wick, Pollock, Jefferson, and Flanagan (2006) describe how the research also supports extending the interest device into the workplace in order to increase performance when the learners apply their new skills to the job. This is accomplished by having the learners and their managers discuss what they need to learn and be able to perform when they finish the training. This pre-class activity ends in a mutual contract between the learners and managers on what is expected to be achieved from the learning process.

The reason this works is that workers often perform what their managers stress, and tend to ignore what their managers ignore.

2. Provide a Learning Objective: This allows the learners to organize their thoughts on what they will learn and perform. There is an old saying among presentation professionals to tell them what you're going to tell them, tell them, and finally tell them what you told them. This works by helping to cue the learner on the goals of the instruction and how they will be able to use their new skills in the workplace.

The problem that some instructors run into is telling the learners the formal Learning Objectives word for word, rather than breaking it down into a less formalized statement. Learning Objectives are normally designed for the instructional designers and trainers, rather than the learners, thus they must be transformed into a more causal language.

Marzano (1998, p.94) reported an effect size of 0.97 (which indicates that achievement can be raised by 34 percentile points) when goal specification is used. When students have some control over the learning outcomes, there is an effect size of 1.21 (39 percentile points).

3. Stimulate recall of prior knowledge: This allows the learners to use two important learning processes:

Taking practice tests allows learners to retrieve and reconstruct their knowledge. Remembering information we are organizing allows us to create patterns, cues, and connections that our brains can recognize.

Scaffolding is the support that a skilled performer gives her apprentices in carrying out a task (Collins, Brown, Holum, 1991). It is accomplished by building upon the student's prior learning. The basic steps of scaffolding include:

  1. Start by building on what the learners already know
  2. Add more details and information over a period of time
  3. Allowing the learners to perform on their own
  4. Afterwards, the fading process begins by slowly removing the support in order to give the learners more responsibility.

In addition, part of stimulating recall is having the learners take notes and drawing mind maps. Learning is enhanced by encouraging the use of graphic representations when taking notes (mind or concept maps). While normal note-taking has an overall effect size of .99, indicating a percentile gain of 34 points, graphic representations (mind maps) produce a percentile gain in achievement of 39 points (Marzano, 1998).

One of the most effective of these techniques is semantic mapping or concept mapping. With this technique, the learner represents the key ideas in a lesson by drawing nodes (circles) with spokes depicting key details emanating from the node. Having the learners draw a semantic map produces an effect size of 1.48 (n=1), indicating a percentile gain of 43 points (Toms-Bronowski, 1982).

4. Present the material: Sequence and chunk the information to avoid cognitive overload. Blend the information to aid in information recall. This is directly related to Skinner's sequenced learning events by allowing the learners to receive feedback on individualized tasks, thereby correcting isolated problems rather than having little idea of where the root of the learning challenge lies. Bloom's Taxonomy and Learning Strategies can be used to help sequence the lesson by helping you chunk them into levels of difficulty.

5. Provide guidance for learning: Provide coaching on how to learn the skill. The rate of learning increases because learners are less likely to lose time and become frustrated by practicing the wrong way or using poorly understood concepts. Coaching the learners to learn-to-learn also has the benefit of helping them to gain metacognitive skills that will aid them with future performance initiatives.

6. Elicit performance: Practice by letting the learner do something with the newly acquired behavior, skills, or knowledge.

In addition, demonstrate as required (modeling). Albert Bandura (1997) noted that observational learning may or may not involve imitation. For example if you see someone driving in front of you hit a pothole, and then you swerve to miss it, you learned from observational learning, not imitation (if you learned from imitation then you would also hit the pothole). What you learned was the information you processed cognitively and then acted upon. Observational learning is much more complex than simple imitation. Bandura's theory is often referred to as social learning theory as it emphasizes the role of vicarious experience (observation) of people affecting people (models). Modeling has several affects on learners:

7. Provide feedback: This can be a test, quiz, or verbal comments. The feedback needs to be specific, rather than something similar to “you are doing a good job.” Tell them why they are doing a good job and/or provide specific guidance.

8. Assess performance: Evaluate the learners to determine if the lesson has been learned and provide general progress information.

9. Enhance retention and transfer: Inform the learners about similar problem situations, provide additional practice (see over-learning below), put the learners in a learning transfer situation, and review the lesson.

Rethinking Gagnes Nine Steps of Instructional Design
View more presentations from Donald Clark.

Over-Learning

The Army Research Institute on Behavioral and Social Sciences (Zipperer, Klein, Fitzgerald, Kinnison, Graham, 2003) completed a meta-analysis of the effects of over-learning — additional training for the learner that occurs after the learner has reached proficiency on the task.

The results of the analysis indicate that over-learning produces reliably better retention of the skill than just training to proficiency. Even after thousands of practice trials, over-learning produces reliably better retention of the skill than just training to proficiency. Apparently, when considering the amount of practice — no amount is ever too much, especially for fundamental skills.

Next Steps

The major instructional design theories and/are models include:

Some other models for creating learning processes are:

References

Bandura, A. (1997). Social Learning Theory. Englewood Cliffs, NJ: Prentice Hall.

Butler, A.C. (2010). Repeated testing produces superior transfer of learning relative to repeated studying. Journal of Experimental Psychology: Learning, Memory, and Cognition, Vol 36(5).

Collins, A., Brown, J.S., Holum, A. (1991). Cognitive apprenticeship: Making thinking visible. American Educator, 6-46.

Gagné, R. (1985). The Conditions of Learning and the Theory of Instruction (4th ed.). New York: Holt, Rinehart, and Winston.

Good, T., Brophy, J. (1990). Educational Psychology: A realistic approach. p.200. New York: Holt, Rinehart, & Winston.

Karpicke, J.D., Janell, R. (2011). Retrieval Practice Produces More Learning than Elaborative Studying with Concept Mapping. Science, 331: 772–775.

Marzano, R.J. (1998). A theory-based meta-analysis of research on instruction. Mid-continent Regional Educational Laboratory, Aurora, CO.

Toms-Bronowski, S. (1982). An investigation of the effectiveness of semantic mapping and semantic feature analysis with intermediate grade level children. Wisconsin Center for Education Research, The University of Wisconsin, Madison, WI.

Wick, C., Pollock, R., Jefferson, A., Flanagan, R. (2006). Six Disciplines of Breakthrough Learning: How to Turn Training and Development Into Business Results. San Francisco: Pfeiffer

Zipperer, E., Klein, G., Fitzgerald, R., Kinnison, H., Graham, E., (2003). Training and Training Technology Issues for the Objective Force Warrior. U.S. Army Research Institute for the Behavioral and Social Sciences: Research Report 1809. Retrieved from: http://www.hqda.army.mil/ari/pdf/rr-1809.pdf